Cách chứng minh hình bình hành
Hình bình hành được gọi là "parallelogram" trong tiếng Anh. Từ "parallelogram" xuất phát từ hai từ "parallel" (song song) và "gramma" (góc), để chỉ rằng các cạnh đối diện của hình bình hành luôn song song và các góc bên trong của nó đều bằng nhau.
Hình bình hành có một số tính chất quan trọng, bao gồm:
- Các cạnh đối diện của hình bình hành là song song và có độ dài bằng nhau.
- Các góc bên trong của hình bình hành đều có độ lớn bằng nhau và bằng 180 độ.
- Đường chéo của hình bình hành cắt nhau tại một điểm giữa, và độ dài của hai đường chéo bằng nhau.
- Hình bình hành có đối xứng qua trục đi qua trung điểm của hai đường chéo.
- Hai góc đối diện của hình bình hành là bù nhau, có tổng bằng 180 độ.
- Diện tích của hình bình hành có thể tính bằng cách nhân độ dài một cạnh với độ dài đường cao tương ứng.
- Chu vi của hình bình hành có thể tính bằng cách cộng độ dài các cạnh.
Các tính chất này giúp chúng ta hiểu và làm việc với hình bình hành một cách dễ dàng. Chúng cũng hữu ích trong việc tính toán, đánh giá và giải quyết các bài toán liên quan đến hình bình hành trong các lĩnh vực như hình học, đồ họa, xây dựng, thiết kế, và nhiều lĩnh vực khác.Xem thêm: Cách chứng minh hình thang 
Hình bình hànhQuy tắc về hình bình hành bao gồm:
- Quy tắc về các cạnh đối diện: Các cạnh đối diện của hình bình hành là song song và có độ dài bằng nhau.
- Quy tắc về các góc: Các góc bên trong của hình bình hành đều có độ lớn bằng nhau và bằng 180 độ.
- Quy tắc về đường chéo: Hai đường chéo của hình bình hành cắt nhau tại một điểm giữa, và độ dài của hai đường chéo bằng nhau.
- Quy tắc về đối xứng: Hình bình hành có đối xứng qua trục đi qua trung điểm của hai đường chéo.
- Quy tắc về góc đối diện: Hai góc đối diện của hình bình hành là góc bù nhau, có tổng bằng 180 độ.
- Quy tắc về diện tích: Diện tích của hình bình hành có thể tính bằng cách nhân độ dài một cạnh với độ dài đường cao tương ứng.
- Quy tắc về chu vi: Chu vi của hình bình hành có thể tính bằng cách cộng độ dài các cạnh.
- Các quy tắc này giúp chúng ta hiểu và áp dụng các thuộc tính và tính chất của hình bình hành trong việc giải quyết các bài toán và vấn đề liên quan đến hình học và các lĩnh vực khác.
Có một số cách để chứng minh rằng một hình là hình bình hành. Dưới đây là một số cách phổ biến để chứng minh tính chất của hình bình hành:
3.1. Chứng minh tứ giác là hình bình hành khi có 2 cặp cạnh đối song song
✔ Cho hình bình hành ABCD. Có AB // DC & AD // BC <=> ABCD là hình bình hành (theo tính chất tứ giác có các cặp cạnh đối song song với nhau là hình bình hành).
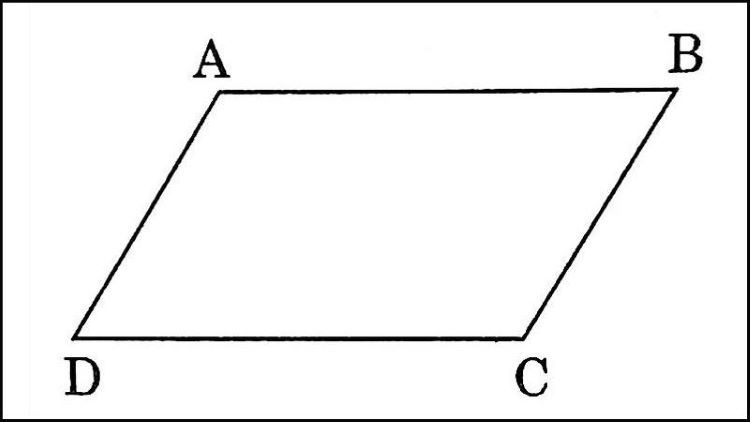
Tứ giác có hai cặp cạnh đối song song là hình bình hành3.2. Chứng minh tứ giác là hình bình hành khi có các cặp cạnh đối bằng nhau
✔ Cho tứ giác ABCD. 2 đường chéo AC và BD cắt nhau tại O. Có tam giác ABC và tam giác ADC:
AD = BC
AB = CD
Chứng minh:
✔ Ta có cạnh chung giữa hai tam giác ABC và ADC là AC => Tam giác ABC = tam giác ADC (theo tính chất cạnh.cạnh.cạnh)
✔ Khi hai tam giác bằng nhau, suy ra:
Góc BAC = góc DAC (góc tương ứng). Mà 2 góc này ở vị trí so le trong => BC // AD (1)
Góc CAB = góc ACD (góc tương ứng). Mà 2 góc này ở vị trí so le trong => DC // AB (2)

Tứ giác có các cặp cạnh đối bằng nhau là hình bình hành3.3. Chứng minh tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành
✔ Từ định nghĩa, tính chất của hình bình hành, ta có:
AB // CD
AB = CD
AI = IB
DK = KC
=> AI // KC và AI = KC
3.4. Chứng minh tứ giác có 2 cặp góc đối bằng nhau là hình bình hành
✔ Cho tứ giác ABCD có tam giác ABD = tam giác BCD & tam giác ABC = tam giác ADC.
✔ Từ đây ta có:
Tam giác BCD = tam giác BAD (theo lý thuyết) => góc BCD = góc BAD (1)
Tam giác ABC = tam giác ADC (theo lý thuyết) => góc ABC = góc ADC (2)
✔ Từ (1) và (2), do các góc đối bằng nhau nên ta chứng minh được tứ giác ABCD là hình bình hành.
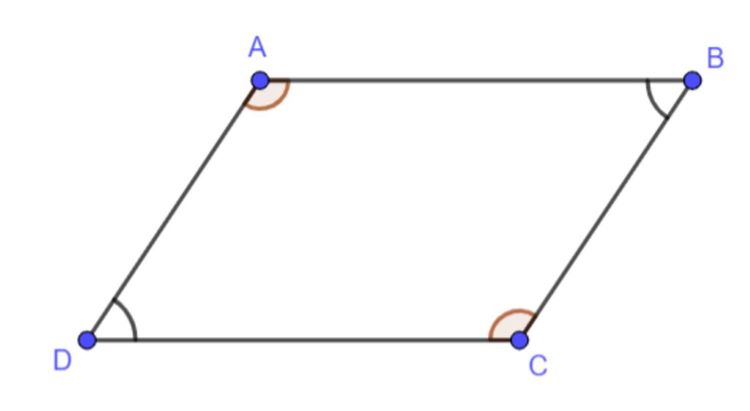
Tứ giác có 2 cặp góc đối bằng nhau là hình bình hành3.5. Chứng minh tứ giác có hai đường chéo cắt nhau tại trung điểm là hình bình hành
✔ Tứ giác ABCD có AC cắt BD tại I => I là trung điểm của AC và BD.
Ta có IA=IC và IB=ID.
Chứng minh:
✔ Xét tam giác AID và tam giác CIB có:
IA = IC
Góc AID = góc BIC (đối đỉnh)
IB = ID
=> tam giác AID = tam giác CIB (theo tính chất cạnh – góc – cạnh)
=> AD = BC (1).
Góc DAI = góc BCI => AD // BC (2)
✔ Từ (1) và (2) => tứ giác ABCD là hình bình hành.

Tứ giác có 2 đường chéo cắt nhau ở trung điểm mỗi đường là hình bình hànhTrên đây là các cách chứng minh hình bình hành đơn giản nhất. Hy vọng qua bài viết sẽ giúp được bạn hiểu thêm về hình bình hành nhanh chóng nhất. Chúc bạn thành công nhé!